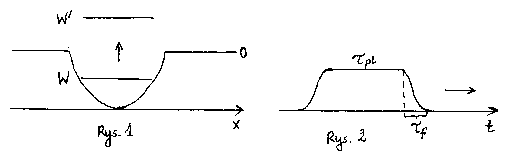
Klasyczny model atomu. Atom jest układem kwantowym i dlatego jego oddziaływanie z polem świetlnym powinno być rozpatrywane z punktu widzenia mechaniki kwantowej. Jednak wiele szczególnych cech zachowania się takiego układu można przeanalizować posługując się przybliżeniem klasycznym.
Dajemy pod rozwagę jednowymiarowy model atomu z jednym
elektronem, w którym oddziaływanie elektronu z jądrem jest określone
potencjałem
V(x) = - Voexp{- [(x/ao)2 +
b2]1/2}/[(x/ao)2 + a2]1/2,
gdzie Vo = 676 eV, ao = 0,529 A (angstrem), a = 6,27, b = 4.
W tych warunkach elektron może wykonywać drgania, których amplituda jest określona przez jego energię. Schemat takiego układu przedstawia jakościowo rys. 1, na którym zaznaczono poziom energii W elektronu w atomie. Dla dalszej analizy zakłada się, że energia początkowa elektronu jest równa W = 0,75 eV.
Należy zauważyć, że stanowi związanemu w atomie odpowiada ujemna energia całkowita, natomiast stan o energii całkowitej W > 0 odpowiada sytuacji, gdy elektron oddala się z obszaru występowania potencjału (zob. rys. 1). Proces przechodzenia w takie stany ze stanów związanych nosi nazwę fotojonizacji.
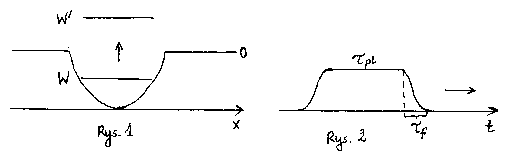
Pole świetlne. W optycznym zakresie częstotliwości ruch elektronu w
atomie jest nierelatywistyczny, dlatego można zaniedbać składową
magnetyczną siły Lorentza, a natężenie pola elektrycznego fali można
uznać za przestrzennie jednorodne E = Eo(t)*cos (omega t), gdzie Eo(t) jest
obwiednią impulsu świetlnego, omega jest częstością kołową pola laserowego.
Kształt impulsu przedstawiono na rys. 2 i jest on opisany wyrażeniem
| Eo(t)= | Eo*sin2 (pi t/(2 tauf)),
Eo, Eo*sin2(pi/(2 tauf)(t - taupl -2 tauf)), | 0 < t < tauf
tauf < t < taupl + tauf taupl+tauf < t < taupl+2 tauf, |
Należy zwrócić uwagę, że w zależności od warunków początkowych (współrzędnej elektronu i jego prędkości) przy jednych i tych samych parametrach impulsu laserowego ruch elektronu może się odbywać w różny sposób. W szczególności przy jednej i tej samej wartości natężenia pola jonizacja może zachodzić lub nie zachodzić. W tym sensie mówi się o prawdopodobieństwie jonizacji atomu.
Zadanie:
1) Zbadać zależność prawdopodobieństwa jonizacji od natężenia
promieniowania P = cEo2/(8 pi) w zakresie natężeń
do 1016 W/cm2,
zakładając, że częstość kołowa pola laserowego omegaKF =
7,62*1015 s-1.
Taka wartość częstości odpowiada częstości promieniowania
ekscymerowego lasera KrF. Przyjąć, że tauf = 5T, taupl = 10T,
gdzie T = 2 pi/omegaKF.
2) Zbadać zależność prawdopodobieństwa jonizacji od częstości
promieniowania w zakresie od 0,1 omegaKF do
omegaKF dla
P = 1013, 1014, 1015
W/cm2. Przyjąć, że tauf = 5T, taupl =
10T, gdzie czas T jest
określony przez wartość minimalnej częstości 0,1 omegaKF.
3) W warunkach zadania 1 zbadać rozkład energii fotoelektronów (tych
elektronów, które oderwały się od atomu).
Uwaga. We wzorach zastosowano absolutny układ jednostek Gaussa.
1 eV = 1,6*10-12 erg = 1,6*10-19 J.
Uwagi dodatkowe:
Warszawa, 11.12.2000.